Unit 3- Geometry of Binary threshold Neuron and
their Networks
Pattern recognition is the process of
recognizing patterns by using a machine learning algorithm.
Pattern recognition can be defined as the
classification of data based on knowledge already gained or on statistical
information extracted from patterns and/or their representation.
Pattern recognition possesses the
following
Pattern recognition system should
recognize familiar patterns quickly and accurate
Recognize and classify unfamiliar objects
Accurately recognize shapes and objects
from different angles
Identify patterns and objects even when
partly hidden
Classification
Classification is defined as the process
of recognition, understanding, and grouping of objects and ideas .
its
pre-categorized training datasets, classification in machine learning programs
leverage a wide range of algorithms to classify future datasets into respective
and relevant categories.
Types of Data Classification
1)Binary Classification
Binary classification involves splitting
items into only two classes. The example above was binary classification, as it
split the reviews into “positive” and “negative”.
Another example of binary classification
is spam filtering, as an email is either classified as “spam” or “not spam”.
2)Multi-Class Classification
This is a classification algorithm that
allows for more than two classes.
During the labelling process, each data
sample is only assigned to a single label.
For example, a recycling centre needs to
categorise each item of waste by taking photographs of the waste travelling
down a conveyor belt.
Rather than categorizing an item as recyclable
or non-recyclable, a multi-class classification model allows a wider range of
classes, such as glass, plastic, paper or cardboard.
3)Multi-Label Classification
This can be used for problems where a single
data point can have more than one class.
For example, a person categorizing images
of animals can label a picture of a brown bear with multiple labels such as
“brown animal”, “furry” and “bear”.
In effect, these systems make multiple
binary classification predictions for each piece of data.
Convex and Convex Hull
A convex set is defined as a set of points in which the line AB connecting any two points A, B in the set lies completely within that set.
What is a Non-convex Set?
Non-convex sets are those that are not
convex.
A non-convex polygon is occasionally
referred to as a concave polygon, and also some sources use the phrase concave
set to refer to a non-convex set.
In diagram (A) is Convex Set (B) is Non-Convex
Set
What is Convex Hull?
The shortest convex set that contains x is
called a convex hull.
In other words, if S is a set of vectors
in En, then the convex hull of S is the set of all convex combinations of every
finite subset of S, and it is represented as [S].
Linear separable means that there is
a hyperplane
This means that there is a hyperplane,
which splits your input data into two half-spaces such that all points of the
first class should be in one half-space and other points of the second class
should be in the other half-space.
In two dimensional space, it means
that there is a line, which separates points of one class from points of the
other class.
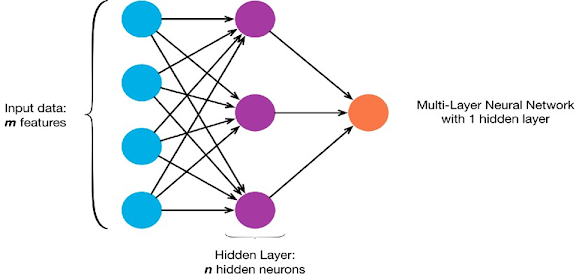
Multi-Layer Neural Network
A multi-layer neural network contains more
than one layer of artificial neurons or nodes. They differ widely in design. It
is important to note that while single-layer neural networks were useful early
in the evolution of AI, the vast majority of networks used today have a
multi-layer model.
Multi-layer neural networks can be set up
in numerous ways. Typically, they have at least one input layer, which sends
weighted inputs to a series of hidden layers, and an output layer at the end.
These more sophisticated setups are also associated with nonlinear builds using
sigmoids and other functions to direct the firing or activation of artificial
neurons. While some of these systems may be built physically, with physical
materials, most are created with software functions that model neural activity.
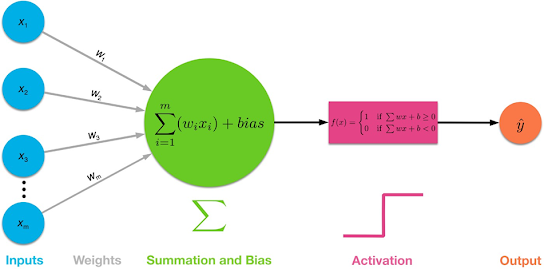
Multi-Layer Neural Network keys: input
data, weights, summation and adding bias, activation function (specifically
step function), and then output.
Back-propagating Learning Algorithms representations
by back-propagating errors:
Backpropagation, a procedure to repeatedly
adjust the weights so as to minimize the difference between actual output and
desired output
Hidden Layers, which are neuron nodes
stacked in between inputs and outputs, allowing neural networks to learn more
complicated features (such as XOR logic)
Network can learn from the difference
between the desired output (what the fact is) and actual output (what the
network returns) and then send a signal back to the weights and ask the weights
to adjust themselves.
XOR problem with neural networks
The
XOR gate can be usually termed as a combination of NOT and AND gates
The
linear separability of points
Linear separability of points is the ability to
classify the data points in the plane by
avoiding the overlapping of the classes in the planes. Each of the classes
should fall above or below the separating line and then they are termed as
linearly separable data points. With respect to logical gates operations like
AND or OR the outputs generated by this logic are linearly separable in the
hyperplane
So
here we can see that the pink dots and red triangle points in the plot do not
overlap each other and the linear line is easily separating the two classes
where the upper boundary of the plot can be considered as one classification
and the below region can be considered as the other region of classification.
Need for linear
separability in neural networks
Linear separability is required in neural networks is required as basic
operations of neural networks would be in N-dimensional space and the data
points of the neural networks
Linear
separability of data is also considered as one of the prerequisites which help
in the easy interpretation of input spaces into points whether the network is positive
and negative and linearly separate the data points in the hyperplane.
linear
separable use cases and XOR is one of the logical operations which are not
linearly separable as the data points will overlap the data points of the
linear line or different classes occur on a single side of the linear
line.
we can see that above the linear separable line the red triangle is overlapping with the pink dot and linear separability of data points is not possible using the XOR logic. So this is where multiple neurons also termed as Multi-Layer Perceptron are used with a hidden layer to induce some bias while weight updating and yield linear separability of data points using the XOR logic. So now let us understand how to solve the XOR problem with neural networks.
Solution
of xor problem
The
XOR problem with neural networks can be solved by using Multi-Layer
Perceptron’s or a neural network architecture with an input layer, hidden
layer, and output layer.
To solve this
problem, we add an extra layer to our vanilla perceptron, i.e., we create
a Multi Layered Perceptron (or MLP). We call this
extra layer as the Hidden layer. To build a perceptron, we first
need to understand that the XOr gate can be written as a combination of AND
gates, NOT gates and OR gates in the following way:
a XOr b = (a AND NOT b)OR(bAND
NOTa)
So during the forward propagation through the neural networks, the weights get updated to the corresponding layers and the XOR logic gets executed. The Neural network architecture to solve the XOR problem will be as shown below.
problem
wherein linear separability of data points is not possible using single neurons
or perceptron’s. So for solving the XOR problem for neural networks it is
necessary to use multiple neurons in the neural network architecture with
certain weights and appropriate activation functions to solve the XOR problem
with neural networks.
Milan Tomic
Hi. I’m Designer of Blog Magic. I’m CEO/Founder of ThemeXpose. I’m Creative Art Director, Web Designer, UI/UX Designer, Interaction Designer, Industrial Designer, Web Developer, Business Enthusiast, StartUp Enthusiast, Speaker, Writer and Photographer. Inspired to make things looks better.
0 comments:
Post a Comment